Dominate the Lift: Powerful Rigging and Load Calculation overview

Planning an overhead lift all starts with understanding the weight of the load you plan on lifting and moving. Performing an overhead lift? Then you’d better get an accurate load weight. The load weight will determine the specifications of the equipment used in the lift. Critical equipment used in the lift includes the crane or hoist, crane hook, and the slings and shackles that connect the hook to the load. This article provides an overview of the methods used to determine the weight of a load and two methods for determining rigging and load calculations. The calculations cover load factors, sling angles, and height and length ratios. ( Read more:( Lifting-calc-3-safety-app/ )

Determining Load Weight

One of the very first things you should do before lifting a load at the load calculation stage is determine the total weight of the load. This should be determined in the early planning stages of a lift, as everything else about the overhead lift will need to account for the weight of the load, including:

• Equipment/type of crane being used for the lift
• Type of lifting slings, rigging hardware, and/or below-the-hook devices being used
• Type of sling hitch and sling angle

The total weight of the load must account for every piece of lifting gear involved in the lift, including the hook and everything else below:

• Hook block
• Ropes
• Lifting beams
• Shackles, hoist rings, and other hardware
• Lifting slings

There are a variety of different methods you can use to ( load calculation ) determine the weight of the load, which we will cover in more depth.

Simple Methods to Determine the Weight of a Load

There are many different ways you can easily identify the weight of a load without doing any type of calculations or using specially-engineered load cells or dynamometers.

Look at the Load to See if the Weight is Marked

The load may be marked with the weight by the manufacturer or may have been previously calculated and marked. Look for any visual indications of load weight prior to selecting the appropriate lifting and rigging equipment.

Load Familiarity

If it’s a load that you regularly lift and move through your facility—like a steel coil or a bundle of pipes or lumber—then you will already know the weight of the load. In many instances, your overhead crane was probably designed with a duty cycle and capacity specifically for that repetitive lifting application, so the weight of the load was accounted for when the crane was built.

---

Refer to Engineered Prints or Design Plans

Product prints or engineered drawings of the load may indicate the final assembled weight.

Review Bill of Lading or Shipping Documentation

If the load was shipped or transported to your facility or job site, there should be some type of weight information included on the shipping paperwork you received.

Use an Industrial Scale

For smaller and lighter loads, you may be able to use an industrial floor scale commonly found in production areas or the shipping and receiving department of a facility.

Refer to the Manufacturer’s Specifications or Catalog Data

If the load is a product or piece of machinery, the weight of the load may be indicated on:

• Paperwork provided by the manufacturer
• Information on the manufacturer or distributor’s website
• Product specifications in a catalog or product brochure

Calculating the Weight of a Load

If no load weight information has been provided, then you will need to do some calculations to determine the weight of the load you are going to lift. In this section, we’ll provide you with some basic calculations for calculating the weight of different sized loads of varying material types.

Step 1: Determine the Volume of the Load

Rectangle/Square: Volume = Length x Width x Height

Hollow Cylinder: Volume = 3.14 x Length x Wall Thickness x (Diameter – Wall Thickness)

Complex Shapes: In some instances, imagine the whole object is enclosed in a rectangle and then calculate the volume of that rectangle. Or, break the object into two or smaller rectangles and then calculate the weight of each part and add them together.

Step 2: Determine the Material You’ll Be Lifting

The table below can be used for approximate weight values of common loads and materials:

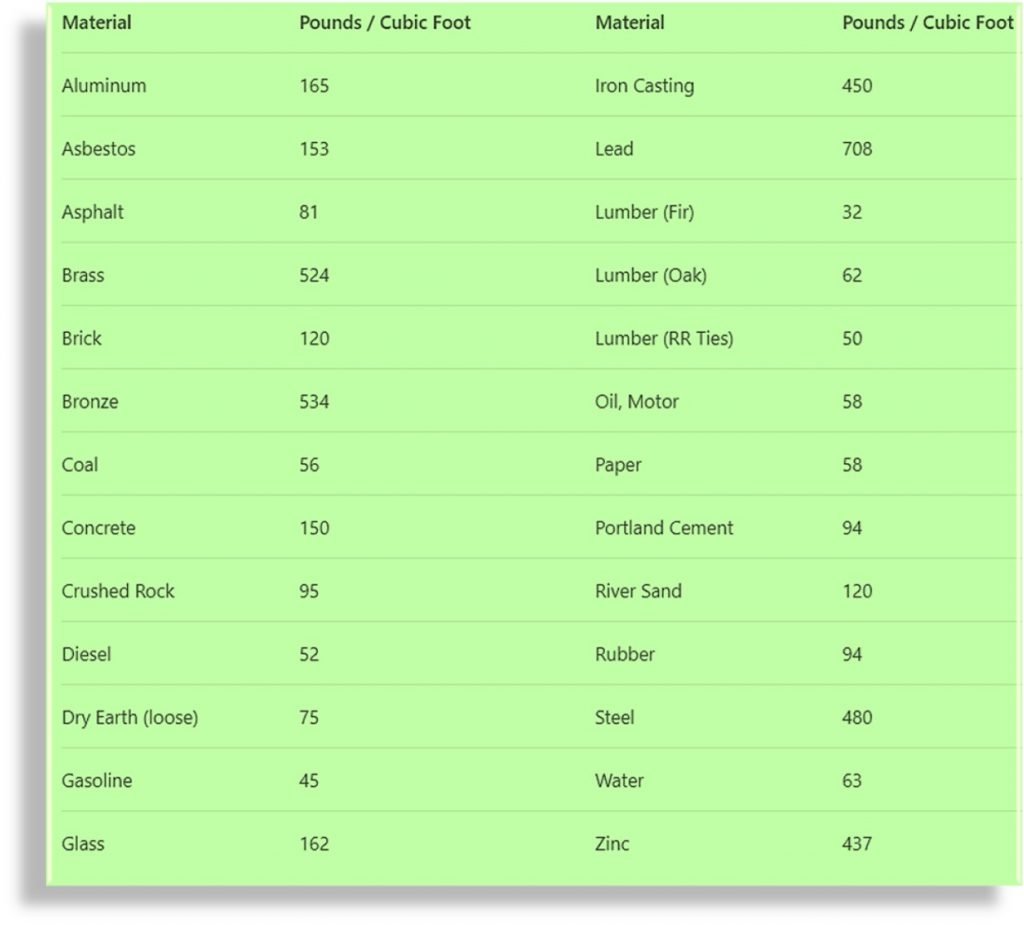
Step 3: Determine the Weight of Object

Multiply the approximate pounds per cubic foot of the material times the calculated volume of the load to get the weight of the object or load.

Example #1: Block of Aluminum

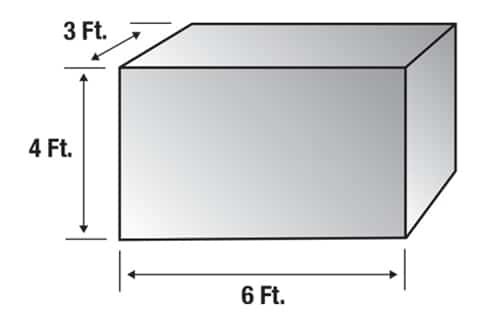
Here’s how you would calculate the load weight of a block of aluminum that is 6 feet long, 3 feet wide, and 4 feet tall:

Volume = Length x Width x Height

Volume = 6 feet x 3 feet x 4 feet

Volume = 72 cubic feet

Aluminum weighs 165 pounds per cubic foot (based on the numbers from the table above). Based on this information, you would perform the following calculation:

Block weight = 72 cubic feet x 165 pounds per cubic feet

Block weight = 11,880 lbs. / 5.94 tons

Example #2: Steel Pipe

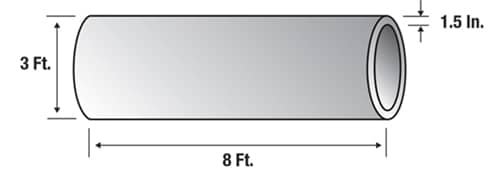
Here’s how you would calculate the load weight of a hollow steel pipe that is 8 feet long, with a 3 foot outside diameter, and wall thickness of 1.5 inches:

Volume = 3.14 x Length x Wall Thickness X (Diameter – Wall Thickness)

Volume = 3.14 X 8 feet x 1.5 inches x (3 feet – 1.5 inches)

Convert inches to feet (1.5 inches = 0.125 feet)

Volume = 3.14 x 8 feet x 0.125 feet x (3 feet – 0.125 feet)

Volume = 3.14 x 8 feet x 0.125 feet x 2.875 feet

Volume = 9.03 cubic feet

Steel weighs 480 pounds per cubic foot (based on numbers from the table above). Based on this information, you would perform the following calculation:

Steel tube weight = 9.03 cubic feet x 480 pounds per cubic foot

Steel tube weight = 4,334 lbs. / 2.17 tons

Example 3: Complex Shapes

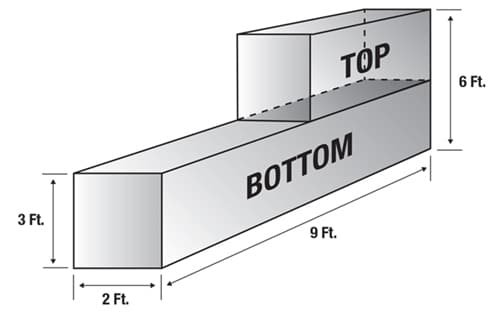
Here’s how you would calculate the load weight of an irregular-shaped object made out of concrete. First, separate the object into rectangles and then calculate the weight of each section individually and then combine them, as shown below:

Volume₁ (Top) = 4 feet x 2 feet x 3 feet

Volume₁ = 24 cubic feet

Volume₂ (Bottom) = 9 feet x 2 feet x 3 feet

Volume₂ = 54 cubic feet

Total Volume = Volume₁ (24 cubic feet) + Volume₂ (54 cubic feet)

Total Volume = 78 cubic feet

Concrete weighs 150 pounds per cubic foot (based on numbers from the table above). Based on this information, you would perform the following calculation:

Complex concrete shape = 78 cubic feet x 150 pounds per cubic foot

Complex concrete shape = 11,700 lbs. / 5.85 tons

Using Load Cells or Dynamometers to Determine Load Weight

Additionally, other devices can be included in the rigging that will provide the operator with a read-out and determination of the load weight when it’s lifted slightly off of the ground. These devices, called load cells or dynamometers, are mounted in line with the crane hook, slings, and hardware. The load is then attached to the load cell and the load cell calculates the weight of the load by measuring the force being applied to it using a strain gauge, or hydraulic or pneumatic pressure inside the device.

These devices can display the measured weight of the load in a variety of ways. Some are mechanical with an analog display that utilizes a needle and dial—similar to how many bathroom or medical scales operate. Others can have digital displays right on the device itself, and some even work with handheld digital devices or computer software to send the readout to an operator who may be performing remote monitoring and diagnostics of the crane equipment.

Another type of load cell device is a load shackle, which is essentially a fully-rated lifting shackle with integrated electronics and microprocessors to determine the weight of a load once lifted into the air. These types of devices also send data to a handheld device or remote workstation.

Many load cells and dynamometers come with overload sensors that alert the operator, safety managers, or other designated personnel if the crane has been overloaded. An overload occurs when a lift exceeds the crane’s rated capacity. Overloads are prohibited according to OSHA and ASME B30 standards and can stress and damage the crane equipment—putting nearby employees in danger if the crane were to fail.

When using load cells or dynamometers, always refer to the manufacturer’s recommendations for scheduled maintenance and calibration to ensure your device is in compliance and continues to provide accurate measurements.

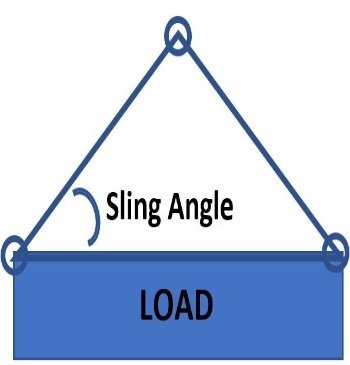
Sling Angles and Loads

After verifying the load weight, the next step will be to calculate the lifting capacity required. The rated lifting capacity of the sling and shackles must be greater than the weight of the load to be lifted.

The force of pull on the leg of a sling varies with the sling angle, so the forces on the sling need to be determined for the specific sling angle used. The sling angle is the internal angle of the sling. As this angle decreases the sling leg load increases.

Example

Let’s look at two methods used to calculate the load on a particular sling leg. One method uses a sling angle factor chart, the other method the ratio of the length of the sling divided by the height.

The sling leg load of two vertical slings is one-half of the total load for each sling. If the load weight is 1000 lbs., the sling load for two vertical slings is:

(1000 lbs. / 2) = 500 lbs for each sling.

As the sling leg angle decreases the force on the sling leg increases. The load factor for the sling angle is taken from a load factor chart.

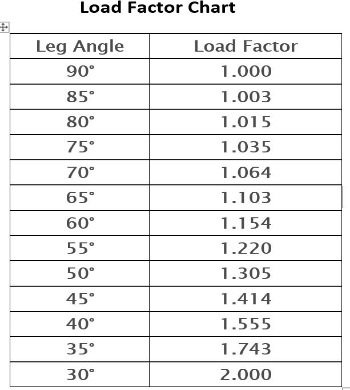
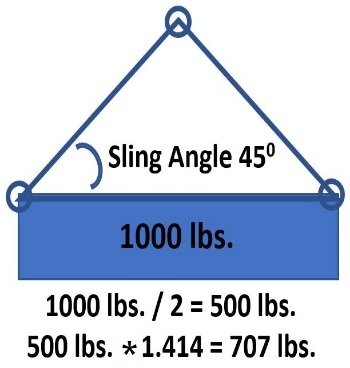
Say two slings are lifting a load of 1000 lbs at an angle of 45 degrees. The load factor from the chart for a 45-degree sling angle is 1.414.

• Sling load force = (load weight / 2) * load factor

(1000 lbs / 2) = 500 lbs
1.414 * 500 lbs = 707 lbs (sling load force)

compare-between-welded-and-mechanical-chain-slings

Note the increase in sling load force as the sling angle decreases.

The ratio of Sling Length vs Height

If you do not have a load chart, you can calculate the sling load factor using the ratio of the sling length divided by the sling height. For this example, we will use a sling length of 28 feet and a height of 20 feet. In this case, the sling load factor would be:

28 / 20 = 1.4

Secure Your Lifts: Guidelines for Safe Lifting Operations Free Planning Tool

wellness and health guidance online